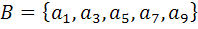پایانترم مبانی ریاضیات پرویزی 1/11/1382 فردوسی مشهد
رای دهی: 5 / 5
به نام خدا
اللهم صل علي محمد و آل محمد
نام آزمون: پايانترم مباني رياضيات
نام استاد: محسن پرويزي
تاريخ برگزاري: 1/11/1382
دانشگاه: فردوسي مشهد
دانشكده: علوم رياضي
رشته: رياضي
1. مفاهيم زير را به دقت تعريف کنيد.
« مجموعه ي متناهي، مجموعه ي ناشمارا، مجموعه ي مرتب جزئي ، کران بالا ، عنصر ماکسيمال »
2. فرض کنيد اعداد طبيعي را با استفاده از اصول پئانو ساخته ايم:
الف: روش ساختن اعداد صحيح را توضيح داده و جمع و ضرب بين آن ها را تعريف کنيد.
ب: ثابت کنيد براي هر دو عدد طبيعي m و n داريم: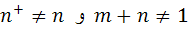 
که در آن 
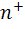تالي n است.
3. فرض کنيد براي هر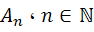 
يک مجموعه ي شماراي نامتناهي باشد، در اين صورت ثابت کنيد 
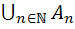نيز شماراي نامتناهي است.
4. فرض کنيد A و B دو مجموعه ي دلخواه باشند، ثابت کنيد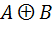 
ناشمارا است اگر و تنها اگر يکي از A يا B ناشمارا باشد.
5. اصل ماکسيمال هاسدورف و لم زرن را بيان نموده و ثابت کنيد اصل ماکسيمال هاسدورف، لم زرن را نتيجه مي دهد.
6. فرض کنيد مي دانيم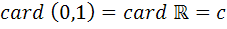 
، در اين صورت ثابت کنيد 
.
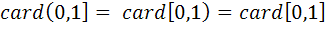7. اعداد اصلي داده شده را مقايسه کنيد: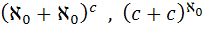 
.
8. ثابت کنيد: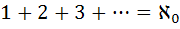 
.
9. ايراد استدلال زير را که ثابت مي کند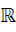 
شماراست، بيابيد.
« فرض کنيد A مجموعه ي تمام زيرمجموعه هاي شماراي 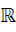باشد. مي دانيم 
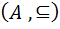يک مجموعه ي مرتب جزئي مي باشد. فرض کنيد 
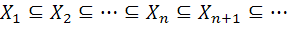يک زنجير در A باشد، به سادگي مي توان ديد که 
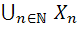يک زير مجموعه ي شمارا از 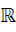است که براي آن داريم :
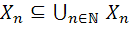
. لذا يک کران بالا براي زنجير داده شده است، حال بنا بر لم زرن A داراي يک عنصر ماکسيمال مانند Y است. بديهي است که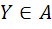 
و لذا شماراست. حال با اثبات اينکه 
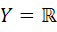اثبات را به پايان مي رسانيم. فرض کنيد 
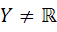لذا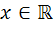 
موجود است که 
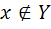. قرار دهيد 
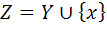واضح است که Z يک زير مجموعه ي شمارا از 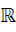است و براي آن داريم 
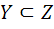که متناقض با ماکسيمال بودن Y مي باشد.»
10. نمودار زير نشان دهنده ي يک مجموعه ي مرتب جزئي مانند A است که در آن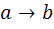 
به معني 
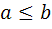مي باشد و 
.
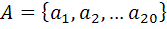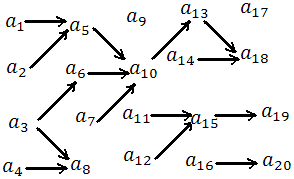
الف: عناصر ماکسيمال ، مينيمال، ماکزيمم و مينيمم مجموعه ي A را در صورت وجود مشخص کنيد.
ب: تمام زنجيرهاي ماکسيمال A را در صورت وجود مشخص کنيد.
پ: با در نظر گرفتن مجموعه ي B ، کران هاي بالا ، کران هاي پايين، سوپريمم و اينفيمم آن را در صورت وجود مشخص کنيد.
