پایان ترم آنالیز حقیقی دانشگاه صنعتی شریف دکتر فتوحی ۱۳۹۲۱۰۱۸
رای دهی: 5 / 5
نام آزمون: پایانترم آنایز حقیقی
دانشگاه: صنعتی شریف
دانشکده علوم ریاضی
نیمسال اول 93-1392
تاریخ برگزاری: 18 بهمن 1392 (13921018)
وقت ۳ ساعت
دانلود فایل PDF پایانترم آنالیز حقیقی دانشگاه صنعتی شریف دکتر فتوحی مورخ 13921018 (همین آزمون)
سؤال ۱. دنباله 
را در
در نظر بگیرید که 
و قرار دهید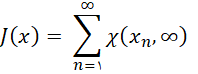 
. ثابت کنید 
تقریباً همه جا وجود دارد و برابر صفر است.
سؤال ۲. عملگر خطی کراندار 
را روی یک فضای هیلبرت در نظر بگیرید. عملگر الحاقی 
را تعریف کزده و وجود آن را اثبات نمایید. هم چنین نشان دهید 
.
سؤال ۳. فرض کنید اندازه های مثبت v و 
روی 
، 
-متناهی باشند. تعریف پیوستگی مطلق v نسبت به را بیان کرده و ثابت کنید که در این شرایط تابع -انتگرالپذیر f وجود دارد که 
. ( استفاده از قضیه رادون-نیکودسم جایز نیست.)
سؤال ۴.دنباله 
در 
تقریباً همه جا به تابع f همگرا است. ثابت کنید 
اگر و تنها اگر 
.
سؤال ۵. اگر 
یک دنباله متعامد یکه در فضای هیلبرت 
باشد و 
یک دنباله از اعداد حقیقی که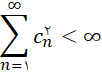 
، نشان دهید مجموعه 
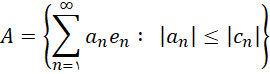در فشرده است.
سؤال 6. اگر v یک اندازه علامتدار -متناهی روی X باشد. نشان دهید مجموعه های اندازه پذیر A و B وجود دارند که 
، 
و برای هر مجموعه اندازه پذیر E
، 
.
(یادآوری: 
و 
که 
اندازه تغییرات کلی v است.)
موفق باشید
