درون‌یابی خطی
رای دهی: 4 / 5
به نام خدا
الهم صل علي محمد و آل محمد
درون‌يابي خطي ساده‌ترين نوع درون‌يابي است. شما با اين درون‌يابي از دوره دبيرستان آشنا شده‌ايد اما هيچ‌گاه نام درون‌يابي بر آن ننهاده‌ايد! اکنون ریاضیات ایران شما را با درون‌يابي خطي آشنا مي کند.
به طور ساده، در درون‌يابي خطي اطلاعات تابع f در دو نقطه‌ي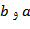 
داده شده است و مي‌خواهيم مقادير تابع را در بازه‌ي 
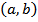درون‌يابي نماييم. تابع درونياب خطي P بين دو نقطه‌ي 
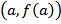و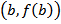 
، به صورت زير است:
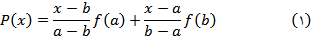
اين تابع، همان معادله‌ي خطي است که از دو نقطه‌ي 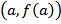و 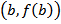مي‌گذرد.
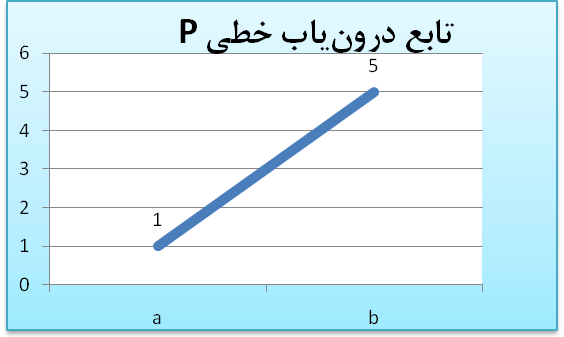
مثلاً فرض کنيد مقدار تابع f در نقاط a و b به ترتيب برابر با 1 و 5 باشد، نمودار تابع درون‌يابي خطي P به صورت شکل زير مي‌باشد:
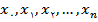داده شده باشد. مي‌خواهيم تابع درونياب خطي را در نقطه‌ي 
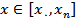بيابيم. براي اين منظور ابتدا کوچکترين زيربازه‌ي 
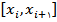که x در آن قرار دارد را مي‌يابيم و سپس تابع درون‌يابي خطي را از فرمول شماره 1 بالا به دست مي‌آوريم.مثال 1: فرض کنيد مقادير تابع f به صورت جدول زير باشد، مقدار تابع را در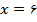 
، با استفاده از درون‌يابي خطي تقريب بزنيد.
|
14
|
13
|
10
|
8
|
7
|
4
|
2
|
 |
|
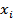18
|
19
|
17
|
16
|
15
|
12
|
11
|
 |
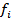حل: همان‌گونه که مشاهده مي‌کنيد، کوچکترين بازه‌اي که
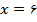در آن قرار دارد بازه‌ي 
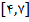مي‌باشد. بنابراين با استفاده از دو نقطه‌ي 4 و 7، تابع درون‌يابي خطي را به دست مي‌آوريم: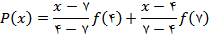
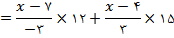
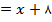
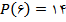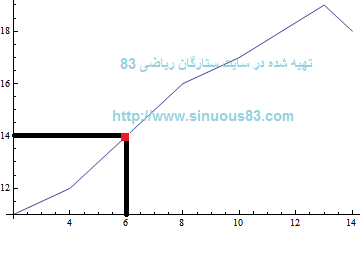
خواهد بود.نمودار اين تابع درون‌يابي در کل بازه به صورت شکل زير است. براي اين کار در هر زيربازه، تابع درونياب خطي را به دست مي آوريم و رسم مي کنيم. بنابراين شکل کلي به صورت يک خط شکسته خواهد بود. همچنين در شکل زير نقطه ي 6 و مقدار آن نمايش داده شده است:
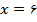مي‌توانستيم از بازه‌هاي ديگري استفاده کنيم. ببينيد در صورتي که از بازه‌هاي ديگر استفاده کنيم چه اتفاقي خواهد افتاد. براي اين که معياري براي مقايسه داشته باشيم، اين بررسي را روي تابع خاصي در مثال بعدي نشان مي‌دهيم.مثال 2: فرض کنيد مقادير برخي نقاط تابع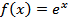 
به صورت جدول زير باشد:
| 6 | 4 | 2 | 1 | 0 | 2- | 4- | 6- |
|
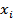| 403.429 | 54.5982 |
7.38906
|
؟ | 1 |
0.135335
|
0.0183156
|
0.00247875
|
 |
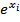مقدار
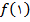را با استفاده از درون‌يابي خطي به دست آوريد.
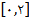را انتخاب مي‌کنيم: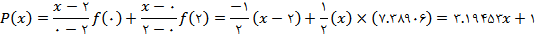 
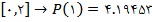
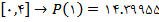
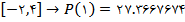
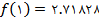مي‌باشد، که با توجه به مقادير بالا مشخص است که هرچه بازه کوچکتر باشد، مقدار تخميني به مقدار واقعي نزديکتر است.در صورتي که بخواهيم همه‌ي بازه را درون‌يابي نماييم، تابع درونياب خطي هر بازه‌ي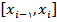 
را به دست مي‌آوريم.
با اين‌که درون‌يابي خطي ساده‌ترين درون‌يابي است، اما در عمل زياد مورد استفاده قرار نمي‌گيرد زيرا خطاي اين درون‌يابي بسيار زياد است.
