ميانترم توابع مختلط دكتر نارنجاني 8/2/1386
نام آزمون : ميانترم توابع مختلط
تاريخ برگزاري : 8/2/1386
نام استاد : دكتر نارنجاني
دانشگاه : فردوسي مشهد
دانشكده : علوم رياضي و آمار
1. با استفاده از تعريف حد ثابت كنيد كه 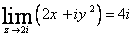 .
.
2. شرط لازم كوشي-ريمان را براي وجود مشتق تابع 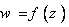 در نقطه ي
در نقطه ي 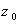 بيان و اثبات كنيد.شرايط كافي را فقط بيان كنيد. تحقيق كنيد كه تابع
بيان و اثبات كنيد.شرايط كافي را فقط بيان كنيد. تحقيق كنيد كه تابع 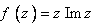 در كدام نقطه داراي مشتق است و مشتق آن را محاسبه كنيد.
در كدام نقطه داراي مشتق است و مشتق آن را محاسبه كنيد.
3. ثابت كنيد كه 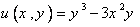 همساز است، مزدوج همساز آن را محاسبه كنيد. تابع تحليلي متناظر
همساز است، مزدوج همساز آن را محاسبه كنيد. تابع تحليلي متناظر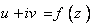 را بيابيد مشروط به آنكه بدانيم
را بيابيد مشروط به آنكه بدانيم 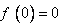 .
.
4. قسمت حقيقي و موهومي تابع w = cos z را محاسبه كنيد و با استفاده از آن يا به طريقي ديگرمعادله ي cos z = 2 را حل كنيد.
5. فرض كنيم 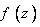 در حوزه ي D پيوسته باشد و به ازاي هر
در حوزه ي D پيوسته باشد و به ازاي هر 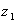 و
و 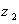 از درون D انتگرال
از درون D انتگرال 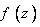 بين
بين 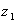 و
و 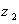 از مسيري كه
از مسيري كه 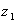 را به
را به 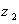 وصل مي كند و درون D است مستقل باشد، ثابت كنيد كه f در D داراي تابع اوليه است.
وصل مي كند و درون D است مستقل باشد، ثابت كنيد كه f در D داراي تابع اوليه است.
6. تابع 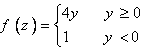 و C قوسي است از منحني
و C قوسي است از منحني 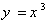 از نقطه ي
از نقطه ي 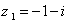 تا
تا 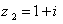 امتداد دارد. مطلوب است
امتداد دارد. مطلوب است 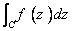 .
.
7. كليه ي مقادير 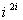 و
و 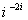 و مقادير اصلي آنها را محاسبه كنيد. ثابت كنيد كه
و مقادير اصلي آنها را محاسبه كنيد. ثابت كنيد كه 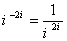 .
.

